Problema:
Dato un insieme I di n intervalli [a, b] con a e b interi determinare il sottoinsieme piu’ grande di intervalli mutuamente non sovrapposti che possono essere selezionati da I.
Input:
Due vettori di n interi che rappresentano l’insieme I.
a = { a0, a1, … }
b = { b0, b1, … }
Ogni intervallo e’ identificato da un numero intero k.
L’intervallo generico k e’ rappresentato dagli estremi a[k] e b[k].
Output:
Una lista di interi ordinata (List<int>) che contiene gli identificatori degli intervalli che fanno parte del sottoinsieme di interesse.
Esempio:
Input:
a = { 0, 7, 15, 2, 8, 15, 18, 3, 10, 12, 15, 1, 4, 8, 20 };
b = { 4, 12, 18, 6, 14, 17, 20, 9, 11, 14, 19, 5, 7, 20, 22 };
Output:
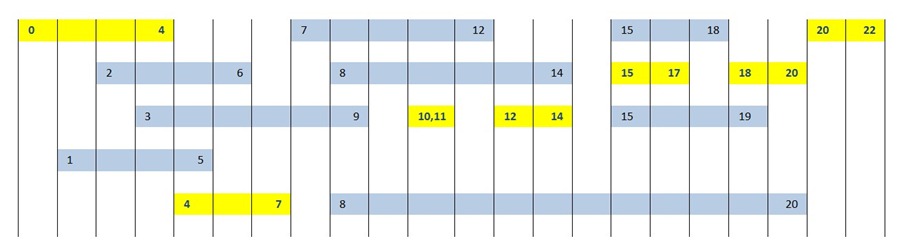
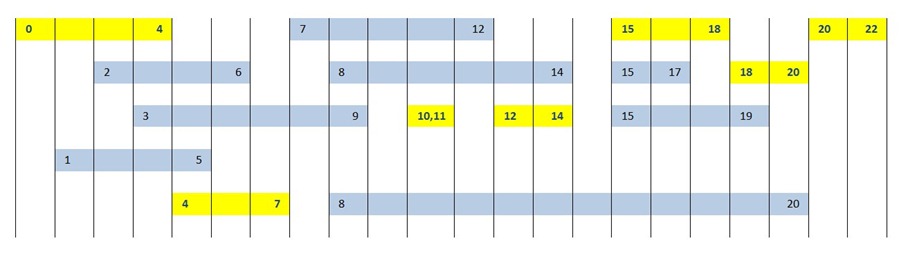
{ 0, 5, 6, 8, 9, 12, 14 } oppure
{ 0, 2, 6, 8, 9, 12, 14 }
Di seguito i diagrammi che rappresentano i due risultati validi (evidenziati in giallo):
Il mio ragionamento:
Per ciascun intervallo determino gli intervalli che si sovrappongono. Ordino quindi gli intervalli in base al numero di sovrapposizioni. Partendo dagli intervalli con il minor numero di sovrapposizioni inizio ad aggiungerli al risultato, scartando a mano a mano gli intervalli sovrapposti.
La complessita’ di questa soluzione e’ O(N^2).
Non sono in grado di provare se questa soluzione e’ corretta per qualsiasi istanza del problema.
La mia soluzione:
class Interval
{
public int ID { get; set; }
public List<int> Overlaps { get; set; }
public bool IsCandidate { get; set; }
public Interval(int interval)
{
ID = interval;
Overlaps = new List<int>();
IsCandidate = true;
}
}
static List<int> GetBiggestNonOverlappedIntervalSubset(int[] a, int[] b)
{
if (a == null) throw new ArgumentNullException("a");
if (b == null) throw new ArgumentNullException("b");
if (a.Length != b.Length) throw new ArgumentException("a and b must have the same length");
int n = a.Length;
List<int> results = new List<int>();
Interval[] intervals = new Interval[n];
for (int i = 0; i < n; ++i)
intervals[i] = new Interval(i);
for (int i = 0; i < n; ++i)
for (int j = i + 1; j < n; ++j)
if (a[i] < b[j] && a[j] < b[i])
{
intervals[i].Overlaps.Add(j);
intervals[j].Overlaps.Add(i);
}
Array.Sort<Interval>(intervals, (info1, info2) => info1.Overlaps.Count - info2.Overlaps.Count);
for (int i = 0; i < n; ++i)
if (intervals[i].IsCandidate)
{
int newInterval = intervals[i].ID;
results.Add(newInterval);
for (int j = i + 1; j < n; ++j)
if (intervals[j].Overlaps.Contains(newInterval))
intervals[j].IsCandidate = false;
}
results.Sort();
return results;
}
I miei test:
Un problema piu’ complesso come questo richiede la presenza di qualche test automatico.
[TestMethod()]
public void GetBiggestNonOverlappedIntervalSubsetTest_DisjointedIntervals()
{
int[] a = new int[] { 0, 6, 10 };
int[] b = new int[] { 4, 8, 12 };
var expected = new List<int> { 0, 1, 2 };
List<int> actual = Program_Accessor.GetBiggestNonOverlappedIntervalSubset(a, b);
Assert.IsTrue(actual.Count == 3);
CollectionAssert.AreEquivalent(expected, actual);
}
[TestMethod()]
public void GetBiggestNonOverlappedIntervalSubsetTest1()
{
int[] a = new int[] { 0, 7, 15, 2, 8, 15, 18, 3, 10, 12, 15, 1, 4, 8, 20 };
int[] b = new int[] { 4, 12, 18, 6, 14, 17, 20, 9, 11, 14, 19, 5, 7, 20, 22 };
var expected1 = new List<int> { 0, 5, 6, 8, 9, 12, 14 };
var expected2 = new List<int> { 0, 2, 6, 8, 9, 12, 14 };
List<int> actual = Program_Accessor.GetBiggestNonOverlappedIntervalSubset(a, b);
Assert.IsTrue(actual.Count == 7);
Assert.IsTrue(ListEquals(actual, expected1) || ListEquals(actual, expected2));
}
[TestMethod()]
public void GetBiggestNonOverlappedIntervalSubsetTest2()
{
int[] a = new int[] { 0, 1, 2, 3, 4 };
int[] b = new int[] { 2, 3, 4, 5, 6 };
var expected = new List<int> { 0, 2, 4 };
List<int> actual = Program_Accessor.GetBiggestNonOverlappedIntervalSubset(a, b);
Assert.IsTrue(actual.Count == 3);
CollectionAssert.AreEquivalent(expected, actual);
}
private bool ListEquals(List<int> a, List<int> b)
{
if (a.Count != b.Count) return false;
int n = a.Count;
for (int i = 0; i < n; ++i)
if (a[i] != b[i])
return false;
return true;
}
Voi come lo avreste implementato? Idee?
Pensate che la mia soluzione sia corretta?
Se no, potete fornire un contro esempio che porta ad un risultato scorretto?