Problema:
Abbiamo una matrice quadrata (N x N) di interi che rappresenta una immagine. Scrivere un algoritmo che ruota l’immagine di 90 gradi in senso orario.
Input:
Una matrice quadrata (N x N) di interi.
Output:
Una matrice quadrata (N x N) di interi.
Esempio:
Input:
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
Output:
57 49 41 33 25 17 9 1
58 50 42 34 26 18 10 2
59 51 43 35 27 19 11 3
60 52 44 36 28 20 12 4
61 53 45 37 29 21 13 5
62 54 46 38 30 22 14 6
63 55 47 39 31 23 15 7
64 56 48 40 32 24 16 8
Il mio ragionamento:
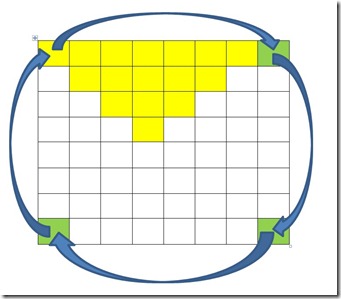
Grazie al fatto che la matrice e’ quadrata non e’ necessario costruire una nuova matrice e poi copiare gli elementi in modo opportuno. E’ possibile effettuare la rotazione sul posto. L’algoritmo e’ scomposto in un certo numero di microrotazioni ciasuna delle quali coinvolge 4 elementi. L’insieme degli elementi di partenza di ciascuna microrotazione deve essere scelto accuratamente per assicurare che tutte le microrotazioni coinvolgano elementi diversi dell’immagine e quindi che ogni elemento venga spostato una volta sola.
Questa immagine mostra evidenziati in giallo gli elementi di partenza delle microrotazioni nel caso di una immagine 8 per 8. Inoltre viene mostrata la microrotazione che coinvolge il primo elemento in altro a sinistra.
La mia soluzione:
static void Rotate90Clockwise(int[][] image)
{
if (image == null) throw new ArgumentNullException("image");
int n = image.Length;
for (int i = 0; i < n; ++i)
if (image[i].Length != n)
throw new ArgumentException("image must be a square");
int m = n / 2;
for (int i = 0; i < m; ++i)
{
int maxi = n - i - 1;
for (int j = i; j < maxi; ++j)
{
int maxj = n - j - 1;
int temp = image[i][j];
image[i][j] = image[maxj][i];
image[maxj][i] = image[maxi][maxj];
image[maxi][maxj] = image[j][maxi];
image[j][maxi] = temp;
}
}
Codice di contorno per verificare l’algoritmo:
static void PrintImage(int[][] image)
{
int n = image.Length;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
Console.Write("{0,3} ", image[i][j]);
Console.WriteLine();
}
}
static int[][] CreateImage(int n)
{
int[][] image = new int[n][];
for (int i = 0; i < n; ++i)
image[i] = new int[n];
int color = 1;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
image[i][j] = color++;
return image;
}
Una versione parallela
Come suggerito da Leonardo un algoritmo di questo tipo puo’ essere facilmente reso parallelo in quanto ciscuna microrotazione e’ indipendente dalle altre. Non ho ancora studiato le Parallel Extension di .NET tuttavia ho voluto provare a sostituire un for con un Parallel.For e fare qualche misurazione.
static void Rotate90Clockwise_Parallel(int[][] image)
{
if (image == null) throw new ArgumentNullException("image");
int n = image.Length;
for (int i = 0; i < n; ++i)
if (image[i].Length != n)
throw new ArgumentException("image must be a square");
int m = n / 2;
Parallel.For(0, m, i =>
{
int maxi = n - i - 1;
for (int j = i; j < maxi; ++j)
{
int maxj = n - j - 1;
int temp = image[i][j];
image[i][j] = image[maxj][i];
image[maxj][i] = image[maxi][maxj];
image[maxi][maxj] = image[j][maxi];
image[j][maxi] = temp;
}
});
}
Misurazioni sul mio Dual Core
Per N piccolo la versione non parallela e’ quella migliore. Il valore di N per cui la versione parallela diventa piu’ efficiente e’ intorno a 250.
N Non parallel (sec) Parallel (sec)
50 0,0011197 0,0032796
100 4,51E-05 0,0001689
150 9,8E-05 0,0001268
200 0,0001755 0,0002104
250 0,0002587 0,0002371
300 0,0004086 0,0003414
350 0,0005709 0,0004235
400 0,0007465 0,0005226
450 0,0009816 0,0006658
500 0,0015623 0,0009149
550 0,0016398 0,0011212
600 0,0019129 0,0011746
650 0,0025198 0,0026563
700 0,0032237 0,0022549
750 0,0036323 0,0020962
800 0,0045339 0,0046006
850 0,0050175 0,0031169
900 0,0056665 0,0032344
950 0,0064017 0,0037355
1000 0,0076806 0,0042115
Per N piu’ grandi si puo’ notare come la versione parallela porti ad un miglioramento di circa il 25%.
N Non parallel (sec) Parallel (sec)
1000 0,0077073 0,0073474
2000 0,0332968 0,020059
3000 0,0805194 0,0478967
4000 0,1537109 0,0925035
5000 0,2477418 0,1521573
6000 0,3798181 0,2527799
7000 0,5527379 0,3792611
8000 0,9368898 0,7253927
9000 1,1020627 0,9026483
10000 1,5610223 1,2783356